¿QUÉ SON LOS SÓLIDOS DE REVOLUCIÓN?

SÓLIDOS DE REVOLUCIÓN 

DEFINICIÓN:

Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo,, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.

ROTACIÓN PARALELA AL EJE DE ABSCISAS (EJE X) 

El volumen de un sólido generado por el giro de un área comprendida entre dos gráficas f(x) y g(x) definidas en un intervalo (a, b) alrededor de un eje horizontal, es decir, una recta paralela al eje Ox de expresión y= K siendo K constante.

ROTACIÓN PARALELA AL EJE DE ORDENADAS (EJE Y) 

Éste es otro método que permite la obtención de volúmenes generados por el giro de un área comprendida entre dos funciones cualesquiera, f(x) y g(x), en un intervalo (a, b) alrededor de un eje de revolución paralelo al eje de las coordenadas cuya expresión es x= K siendo K constante positiva. 

MÉTODO DE DISCOS

Si giramos una región del plano alrededor de un eje obtenemos un sólido de revolución.

Para ver como usar el volumen del disco y para calcular el volumen de un sólido de revolución general, se hacen particiones en la gráfica.

Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo, teniendo en cuenta que la suma del Riemann asociada a la partición y que da un volumen aproximando del sólido.

EJEMPLO:

             

CÁLCULO DE REVOLUCIÓN POR EL MÉTODO DE ARANDELA.

Ahora se presenta un método alternativo de calcular el volumen de un sólido de revolución conocido como método de las arandelas o de anillo, con lo cual damos a conocer en que se basa dicho método, presentando algunas fórmulas, teoría y algunos ejemplos para un mejor entendimiento. 

¿QUÉ ES EL MÉTODO DE ARANDELA?

En términos generales este método se utiliza cuando el eje de rotación se encuentra a una distancia de la función que formará el sólido. Este espacio entre el eje y la función crea un hueco en el sólido, por esto mismo se necesita restar el área del hueco al sólido en revolución. 

Este método consiste en hallar el volumen de un sólido generado al girar un región R que se encuentra entre dos curvas. Si la región que giramos para formar un sólido no toca o no cruza el eje de rotación, el sonido generado tendrá un hueco o agujero, las secciones transversales que también son perpendiculares al eje de rotación son arandelas en lugar de discos. 

                                                 
EJEMPLO:

             

LONGITUD DE CURVA
Por longitud de una recta queremos decir: el número de veces que podemos colocar sobre ella un segmento rectilíneo que se toma como una medida de longitud. Sin embargo podemos medir las líneas curvas de la misma manera, puesto que es imposible que el segmento coincida con la curva. 

EJEMPLO:

           

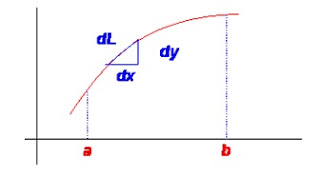
LONGITUD DE UN ARCO DE CURVA
Se define como el límite de la suma de los lados de la poligonal cuando el número de los puntos de división tiendo a infinito, al mismo tiempo que cada uno de los lados tiene a cero.

EJEMPLO:
  
           


OFERTA Y DEMANDA 

La oferta es la cantidad de productos o servicios ofrecidos en el mercado. En la oferta, ante un aumento de precio, aumenta la cantidad ofrecida. 
La demanda es la cantidad de bienes o servicios que los compradores intentan adquirir en el mercado. 

CURVA DE LA OFERTA  

En la curva puede verse como cuando el precio es muy bajo, ya no es rentable ofrecer ese producto o servicio en el mercado, por lo tanto la cantidad ofrecida es 0.

          

   CURVA DE LA DEMANDA

Por medio de la ley de la demanda, se determina que al subir el precio de un bien o servicio, la demanda de éste disminuye. A diferencia de los cambios en otros factores que determinan un corrimiento de la curva en sí).

      

EJEMPLO: